빠른 곱셈 알고리즘 - 1. 카라추바 알고리즘

Computer Science Jun 3, 2025

알고리즘 문제 해결 분야(PS, Problem Solving)에서는 주어진 문제를 정해진 시간/공간 제약 안에 풀기 위한 여러 알고리즘이 사용된다. 특히 가장 초점을 두는 부분은 주어진 문제를 빠른 시간 안에 해결하기 위한 개선된 알고리즘을 찾는 것이며, 보통은 시간복잡도를 기준으로 알고리즘의 성능을 평가한다. 본 포스트의 1편에서는 가장 기본적인 연산인 곱셈을 빠르게 수행하는 알고리즘 중 하나인 카라추바 알고리즘에 대해 다룬다.

기본적인 곱셈 알고리즘

곱셈이 무엇인지 모르는 컴퓨터에게 곱셈을 어떻게 할 수 있는지 설명하는 상황을 생각해보자. 우리가 두 수를 곱할 때 세로셈을 하는 과정을 생각해보면, 두 수의 각 자릿수를 한번씩 비교하며 곱셈한다는 것을 알 수 있다. 이는 진법의 의미를 생각해보면 직관적인데, $57 \times 83 = (5\times 10 ^ {1} + 7 \times 10 ^ {0})\times (8\times 10 ^ {1} + 3 \times 10 ^ {0}) = (5 \times 8) \times 10^{2} + (5 \times 3 + 8 \times 7) \times 10 ^ {1} + 7 \times 3 \times 10 ^ {0} $과 같은 예시를 생각해 볼 수 있다.

이상에서, $n$진법으로 표현된 두 수 $a, b$가 주어졌을 때 두 수를 곱하는 기본적인 알고리즘은 아래와 같이 표현할 수 있다.

multiply(a[1..p], b[1..q], base)
  product = [1..p+q]                                        
  for b_i = 1 to q
    carry = 0
    for a_i = 1 to p
      product[a_i + b_i - 1] += carry + a[a_i] * b[b_i]
      carry = product[a_i + b_i - 1] / base
      product[a_i + b_i - 1] = product[a_i + b_i - 1] mod base
    product[b_i + p] = carry
  return product

또한, 위 알고리즘에 따라 곱셈을 수행할 시 $a, b$의 길이가 각 $n,m$일 때 알고리즘의 시간복잡도는 $O(nm)$이라는 사실도 쉽게 알 수 있다.

시간복잡도의 개선

그런데 과연, 두 수의 곱셈을 $O(nm)$보다 빠르게 수행할 수 있는 방법이 있을까? 잠시 고민해보면 알 수 있겠지만, 두 수의 곱셈을 $O(nm)$보다 빠르게 수행하는 알고리즘을 직관적으로 떠올리기는 쉽지 않다. 실제로 1960년 전까지 두 수를 곱하는 $O(nm)$보다 빠른 알고리즘은 발견되지 않았으며 몇몇 사람들은 $O(nm)$의 시간복잡도가 곱셈 알고리즘의 이론적 하한이라 생각하기도 했다.

그러나 1960년, Anatoly Karatsuba는 이보다 빠른 곱셈 알고리즘이 존재함을 발견했으며, 해당 알고리즘을 카라추바 알고리즘이라 부른다. 카라추바 알고리즘은 $O(n^{\log_2{3}})$의 시간복잡도로 두 수의 곱셈을 수행한다. 평소에 PS 분야에 관심이 있는 사람이라면 아마 시간복잡도가 굉장히 특이하다고 생각될 것이다. 어째서 이런 괴상한 시간복잡도가 나온 것이며, 어떻게 가능할까?

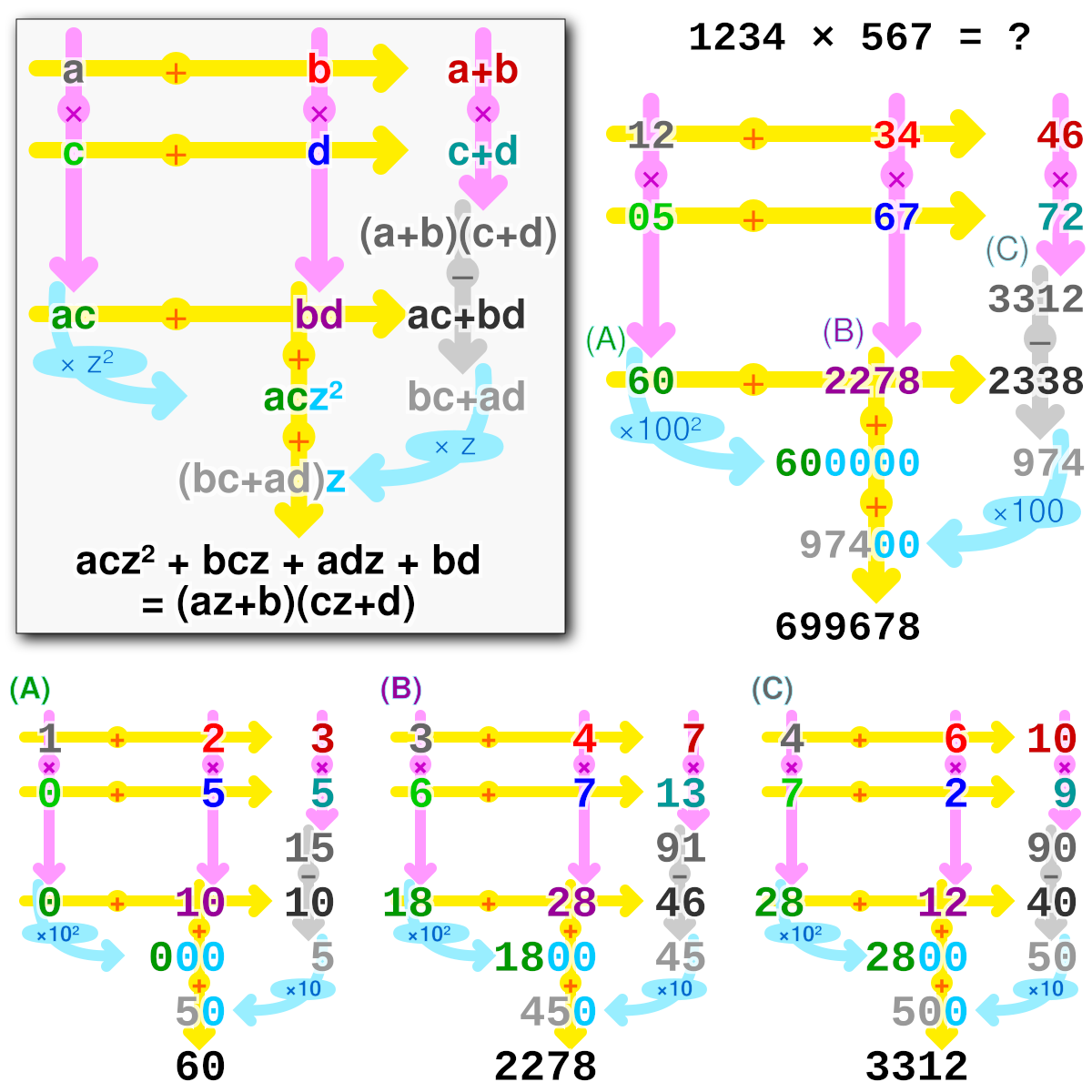
256자리의 수 $a,b$를 생각하자. a와 b는 아래와 같이 표현할 수 있다. $$a=a_{1}\times 10^{128} + a_{0}$$ $$b=b_{1}\times 10^{128} + b_{0}$$

이때 고전적인 곱셈 방식을 이용하면 $$a \times b = (a_1 \times 10^{128} + a_0)(b_1 \times 10^{128} + b_0)$$ $$= a_1b_1 \times 10^{256} + (a_1b_0 + a_0b_1) \times 10^{128} + a_0b_0$$과 같은 식이 유도되며, 이를 계산하기 위해서 4번의 곱셈이 필요하다.

카라추바의 핵심 아이디어는 계산을 위해 필요한 4번의 곱셈을 3번으로 줄일 수 있다는 것이다. $$ z_0 \equiv a_0 \times b_0 \\ z_2 \equiv a_1 \times b_1 \\ z_1 \equiv (a_0 + a_1)(b_0 + b_1) - z_0 - z_2 $$

과 같이 정의한다면, 256자리의 두 수의 곱셈을 128자리 두 수의 곱셈 3개로 나누어 생각할 수 있다. 이를 재귀적으로 반복해서 수행한다면 시간복잡도는 아래와 같은 점화식으로 표현된다. $$T(n)=3T(\frac{n}{2})+O(n)$$ 마스터 정리(Master theorem)를 적용한다면 위 알고리즘의 시간복잡도가 $O(n^{\log_2{3}})$인 것을 알 수 있으며, 이렇게 우리는 기존의 방법보다 빠른 시간복잡도로 두 수를 곱할 수 있는 방법을 알게 되었다!