Ensemble
이 글에서는 Ensemble 이라는 개념에 대해서 알아보자. 필자도 완벽한 이해를 바탕으로 작성하는 글이 아니고, 개념을 소개하는 것에 의의를 두고 있기 때문에 이 주제에 큰 관심이 있는 사람들은 알아서 논문을 더 찾아보기를 바란다.
제목이 굉장히 재미없어 보이지만 나름 재미있는 주제이다. 다들 끝까지 읽도록 하자^^
Introduction
Ensemble 은 열 및 통계 물리학을 배우는데 있어서 꼭 알아야 하는 용어이자 개념이다. 즉, 과학 용어인 것이다. 하지만 조금만 생각해보면 우리가 Ensemble 이라는 단어를 평소에도 쓴다는 것을 알 수 있다. Ensemble 이라는 단어는 사전적으로는 유사한 특성을 갖는 무언가가 모인 집합이다. 통계 역학에서도 비슷한 의미로 쓰인다. 단지 '무언가'가 서로 다른 입자들의 계(system)에 해당될 뿐이다. 입자들이 모인 어떠한 집합이 있을 때, 그 집합이 존재할 수 있는 상태는 굉장히 다양할 것이다. 이때 그러한 상태들의 집합이 Ensemble 이 되는 것이다. 이 글에서는 3가지의 Ensemble 에 대해서 다루게 될 것이다. 바로 Microcanonical Ensemble, Canonical Ensemble, Grand Canonical Ensemble 이다.
Microcanonical Ensemble
Microcanonical Ensemble 은 가장 간단하고 기초적인 Ensemble 이다. Microcanonical Ensemble 의 거시 상태는 고립계와 비슷한 특성을 보인다. 따라서 입자의 개수(N), 부피(V), 에너지(E) 가 일정하다. 미시 상태에서는 H(q, p) (위상 공간에서 특정 위치와 운동량을 가진 입자의 에너지) 가 E < H < E + \(\delta\)E 를 만족해야 한다. 이제 거시 상태와 미시 상태가 각각 무엇인지 알았으니, 둘의 연관성에 대해서 살펴보자. 양자역학에서는 미시 상태의 가짓수가 잘 정의되기 때문에 양자역학의 관점에서 생각해보자. 그렇다면 우리는 하나의 거시 상태에 수많은 미시 상태가 대응된다고 생각할 수 있다. 통계 역학에서는 각 거시 상태에 대응되는 미시 상태의 개수를 상태수(\(\Omega\)) 로 정의한다. 그리고 통계 역학의 기본 가정에 의해 Microcanonical Ensemble 에서는 모든 미시 상태의 존재 확률이 동일하다.
Canonical Ensemble
Canonical Ensemble 은 닫힌계와 비슷한 특성을 보인다. 즉, 입자의 개수(N), 부피(V), 온도(T) 가 일정하다. 이 계에서도 Microcanonical Ensemble 에서 그랬던 것처럼 미시 상태의 존재 확률에 집중할 필요가 있다. Canonical Ensemble 에서는 미시 상태의 존재 확률이 맥스웰 - 볼츠만 분포를 따른다. 증명해보자...!!!!!!
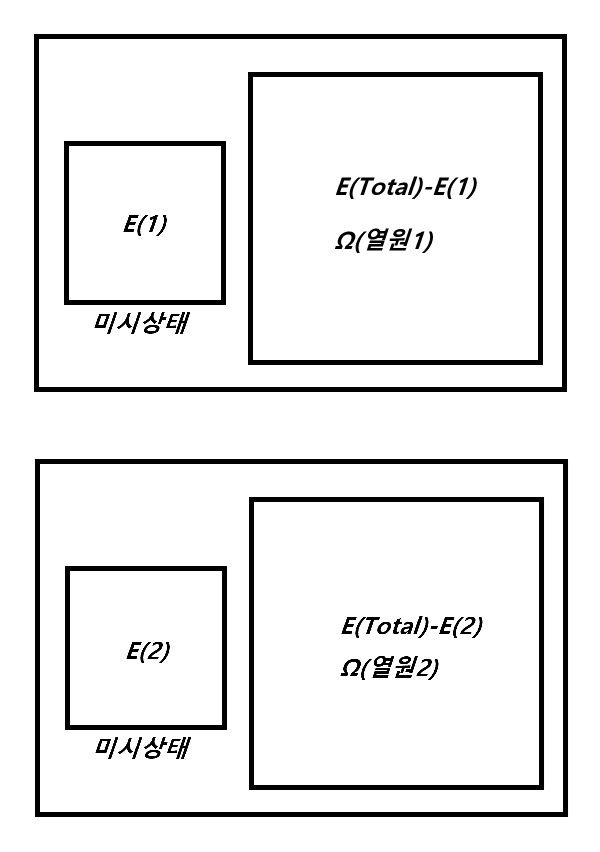
그림에 대한 설명을 조금 하자면, 미시 상태라고 밑에 적혀 있는 박스들이 각각 Canonical Ensemble 을 의미하고, 옆에 있는 조금 더 큰 박스는 온도가 T 인 열원을 나타낸 것이다. 두 박스를 하나로 묶고 있는 가장 큰 박스는 Canonical Ensemble 과 열원을 하나의 계로 표현하기 위한 것이다. 하나의 계로서 관찰을 하게 된다면 각각의 계는 Microcanonical Ensemble 이 된다는 것을 알 수 있다.
두 계에서 Canonical Ensemble 의 미시 상태는 고정이지만, 열원의 미시 상태는 고정이 아니므로 두 계의 미시 상태의 존재 확률 P_1 과 P_2 의 비율은,
\[\frac{P_1}{P_2} = \frac{\Omega_{\text{열원 1}}}{\Omega_{\text{열원 2}}}\] 엔트로피의 정의를 사용하면,
\[\frac{\Omega_{\text{열원 1}}}{\Omega_{\text{열원 2}}} = e^{\frac{S_{\text{열원 1}} - S_{\text{열원 2}}}{k_B}} \] 이때, \(dS = \frac{dE}{T} = \frac{(E_{\text{total}} - E_1) - (E_{\text{total}} - E_2)}{T} = \frac{E_2 - E_1}{T} \) 임을 사용하면, \[ \frac{P_1}{P_2} = e^{\frac{E_2 - E_1}{k_B T}} = \frac{e^{- \frac{E_1}{k_B T}}}{e^{- \frac{E_2}{k_B T}}} \] 따라서, i 에 대해 일반화 해보면, \[\therefore P_{n, \text{미시상태 i}} \propto e^{- \frac{E_i}{k_B T}} \] 이렇게 유도가 가능하다.
Grand Canonical Ensemble
Grand Canonical Ensemble 은 화학 퍼텐셜(\(\mu\)), 부피(V), 온도(T) 가 일정하다. 그렇다! 이 Ensemble 에서는 위에서 소개 했던 것들과 다르게 입자 개수(N) 이 일정하지 않고 교환이 가능하다. 이러한 성질들을 고려하여 계산하면, Grand Canonical Ensemble 에서 미시 상태의 존재 확률은 \(e^{{-\beta}{(E-\mu N)}} \) (\(\beta = \frac{1}{k_B T}\)) 에 비례하게 된다. 이 또한 증명해보자...히히히
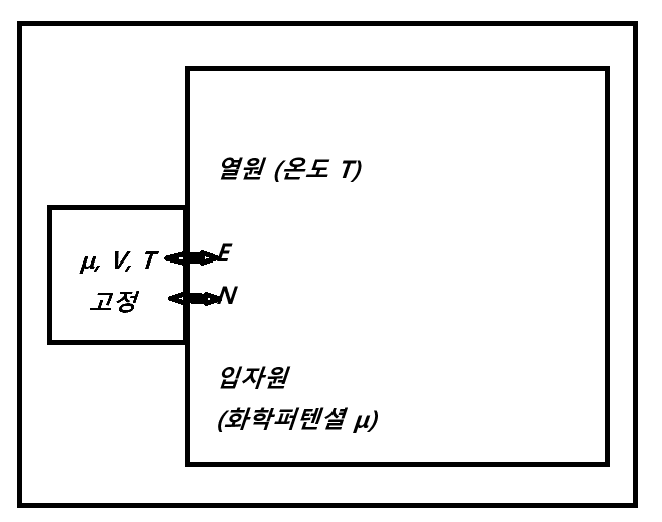
위와 마찬가지로 그림에 대한 설명을 조금 하자면, Canonical Ensemble 에서 증명했던 방법과 비슷한 방법을 사용하기 위해서 억지로 열원과 입자원을 추가하여 계 전체를Microcanonical Ensemble 로 만든 것이다. 그림에서 볼 수 있듯이 가장 작은 박스는 Grand Canonical Ensemble 을 나타내고 그것보다 좀더 큰 박스는 열원과 입자원, 가장 큰 박스는 계 전체를 하나로 묶어 놓은 것이다. 이전과 비슷하게, E_1, N_1 인 Grand Canonical Ensemble 1 과 E_2, N_2 인 Grand Canonical Ensemble 2 가 있다고 하자.
이전에 했던 증명과 비슷하게, Grand Canonical Ensemble 의 미시 상태는 고정이다. 따라서, 열원과 입자원에 대한 상태수만 계산해주면 된다. 두 계의 미시 상태의 존재 확률 P_1 과 P_2 의 비율은, \[\frac{P_2}{P_1} = \frac{ \Omega_{\text{ext}}(E_{\text{tot}} - E_2,\ N_{\text{tot}} - N_2) } { \Omega_{\text{ext}}(E_{\text{tot}} - E_1,\ N_{\text{tot}} - N_1) } \] 엔트로피의 정의를 이용하면, \[\frac{ \Omega_{\text{ext}}(E_{\text{tot}} - E_2,\ N_{\text{tot}} - N_2) } { \Omega_{\text{ext}}(E_{\text{tot}} - E_1,\ N_{\text{tot}} - N_1) } = e^{\frac{ S_{\text{ext}}(E_{\text{tot}} - E_2,\ N_{\text{tot}} - N_2) - S_{\text{ext}}(E_{\text{tot}} - E_1,\ N_{\text{tot}} - N_1) }{ k_B }} \] 여기서 \(dS = \frac{1}{T} dE + \frac{P}{T} dV - \frac{\mu}{T} dN \) 를 사용하면, \[\frac{P_2}{P_1} = e^{\frac{1}{k_B} \left[ \frac{1}{T}(E_1 - E_2) - \frac{\mu}{T}(N_1 - N_2) \right]} = \frac{ e^{-\beta (E_2 - \mu N_2)} }{ e^{-\beta (E_1 - \mu N_1)} } \] 따라서, \[\therefore P \propto e^{-\beta (E - \mu N)}\]
Conclusion
이렇게 이 글에서는 3가지 종류의 Ensemble 에 대해 알아보았다. 필자는 이 분야 공부를 이제 막 시작한 사람이기 때문에 본인의 생각을 정리하고 이 글을 읽는 사람들이 열 및 통계 물리학에 조금이라도 관심을 가지길 바라는 마음으로 이 글을 쓴 것이다. 애매한 내용이나 부정확한 내용이 다수 포함되어 있을 수 있으니 잘 가려서 읽기를 바란다. 그리고 추가적으로 필자에게 도움을 주고 싶은 사람은 댓글에 도움이 될만한 내용들을 적어준다면 굉장히 감사할 것 같다.
마지막으로 더 많은 내용을 알고 싶다면,
https://scholar.harvard.edu/files/schwartz/files/7-ensembles.pdf
참고하세요.