Gamma Function
Introduction
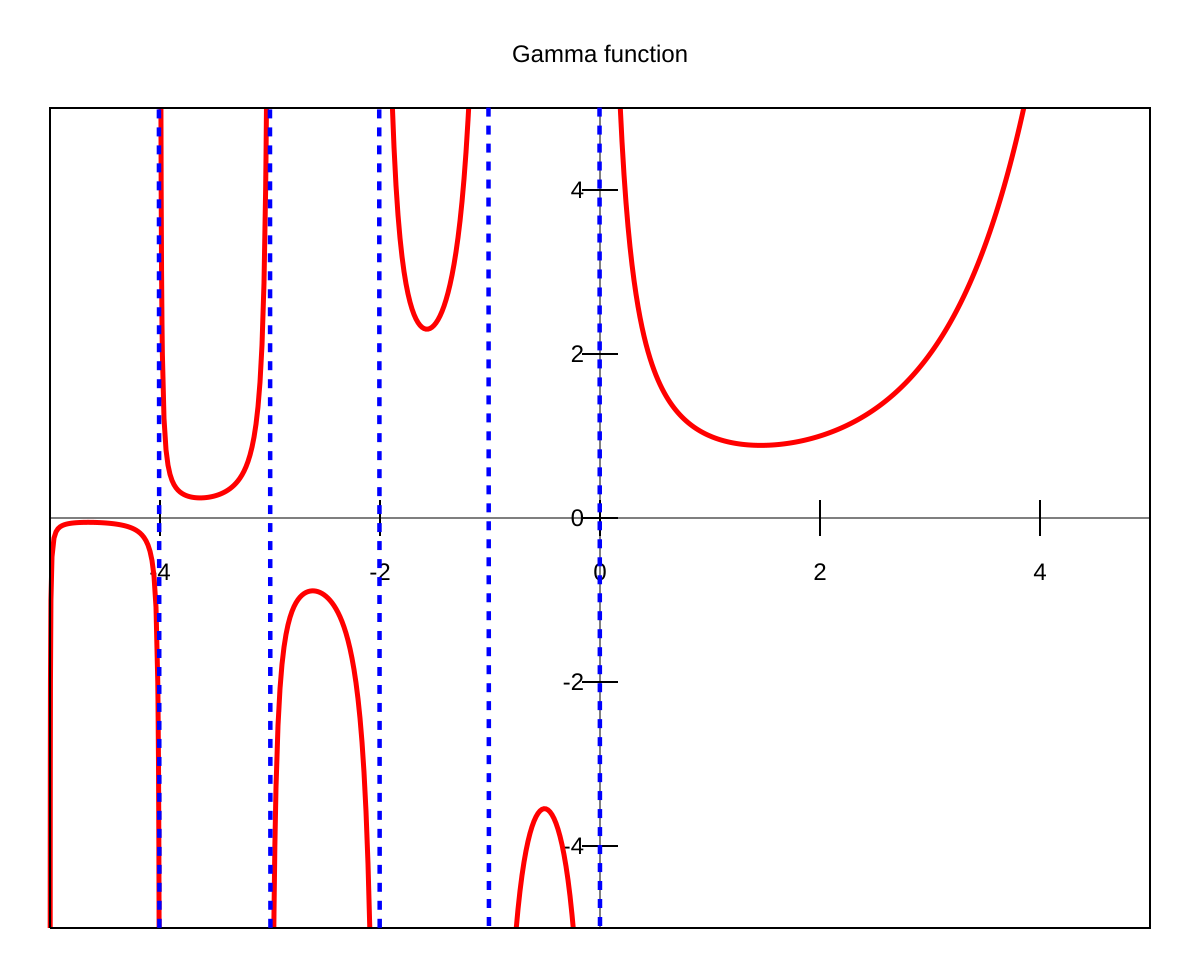
이 글에서는 감마 함수에 대해서 다루기는 하지만, 나중에 쓸 글에 선행되어야 할 지식만 언급을 할 것이기 때문에, 감마 함수의 성질이나 파생된 정리에 대해서는 일절 다루지 않는다. 필자는 감마 함수의 정의만 소개할 것이다. 감마 함수는 나중에 n 차원 구의 표면적을 구할 때 유용하게 사용되기 때문에 잘 알아두도록 하자.
Definition
감마 함수를 정의하는 방법에는 여러가지가 있지만, 앞에서 말했다시피 필자는 미래에 n 차원 구의 표면적을 구할 때 사용되는 것들만 다룰 것이기 때문에 한 가지만 소개하도록 하겠다.
\[\Gamma(z) = \int_0^{\infty} t^{z-1} e^{-t} dt \] (\(Re(z) > 0\))
정확한 정의라고 할 수는 없고 그냥 물리에서는 저 식을 잘 활용하기만 하면 된다. 굳이 수학적으로 엄밀한지는 따지지 말도록 하자.
이제 z 에 z+1 을 대입한 후 식을 부분 적분 해보자. \[\Gamma(z+1) = \int_0^\infty t^z e^{-t} dt = \left[ -t^z e^{-t} \right]_0^\infty + z \int_0^\infty t^{z-1} e^{-t} dt \] \(\left[ -t^z e^{-t} \right]_0^\infty \) = 0 임을 알 수 있다. 따라서 남은 항은, \[z \int_0^\infty t^{z-1} e^{-t} dt = z \Gamma(z) \] 이 식을 통하여, 엄밀하지는 않지만, \[\Gamma(z) = (z-1)! \] 임을 추측할 수 있다.
Conclusion
이 글을 통해 감마 함수가 어떠한 식을 의미하는지 알게 되었다면, 이 글의 목적을 달성한 셈이다. 본론의 마지막 부분에서 언급했다시피 감마 함수는 자연수가 아닌 양의 실수에 대한 factorial 의 일반화로 생각할 수 있다. 이것 또한 꼭 알아두어야 하는 성질이다.
감마 함수에 대해서 더 많이, 엄밀하게 알고 싶다면, 정확성은 보장할 수 없지만, 나름 수학 좋아하는 사람들이 써서 퀄리티는 높다고 생각하는 Wikipedia 를 보도록 하자.
Contributors to Wikimedia projects
