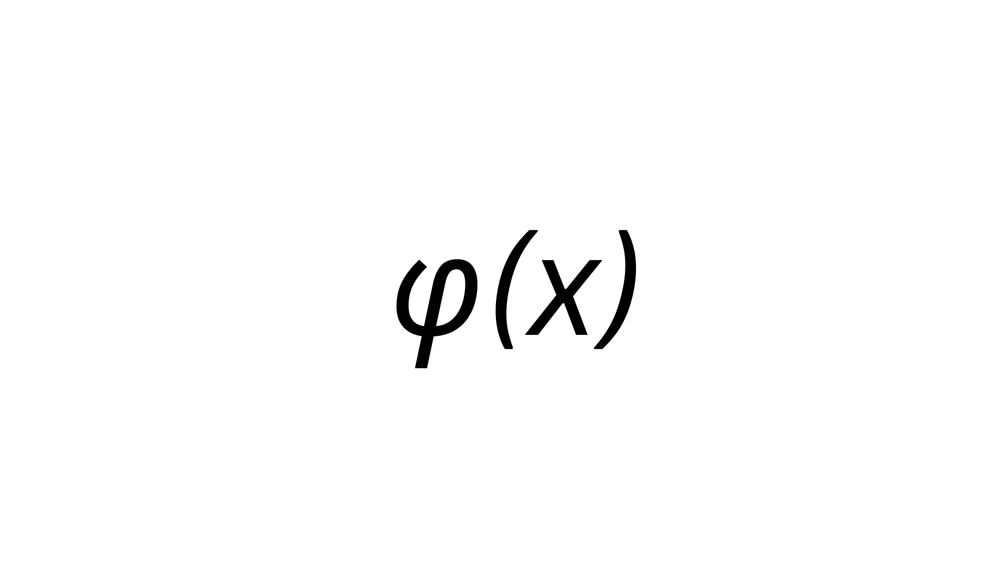오일러 피 함수

Computer Science May 20, 2025

개요

글을 써야지 써야지 하다가 계속 유기를 치게 됐다. 그래서 오늘은 아주 간단한 개념을 소개해서 죄책감을 덜고자 한다. 바로 오일러 피 함수! 수학에서 들어봤을 수도 있다. 그러나 오늘은 정보적으로 접근해보자. (사실 크게 다른 건 없다.)

오일러 피 함수

오일러 피 함수는 아주 간단(?)하다. 일단 무엇인지 알아보자.

오일러 피 함수는 서로소의 개수를 구하는 함수다. 정확히는 자연수 n에 대해서 n보다 작고, n과 서로소인 자연수의 개수를 구해준다. 아래와 같이 나타낼 수 있다.

\[\varphi(n)=|\{m\in N|m<n, gcd(n,m) = 1\}|\]

그럼 이 함수를 자세히 알아보자. 어렵지 않다. 다음 공식만 알면 된다.

\[\varphi(n) = n\prod_{p}({1- \frac{1}{p}}),\ \text{p is a prime factor of n}\]

공식이 성립하는 이유는 당연하다. n 까지의 수 중 p의 배수는 서로소가 아니므로 1에서 1/p를 빼서 그 비율을 맞추는 것이다.

구현

오일러 피 함수를 구현하기 위해서는 소인수를 찾는 프로그램을 먼저 짜야 한다. 근데 이건... 알아서 잘 하겠지...?

소인수를 다 구했으면 for문으로 1-(1/p)를 곱하고 최종적으로 n과 곱해 답을 얻는다. 이때 답이 정수로 나오도록 int()나 \\를 잘 쓰자.

n=int(input())
isprime=[1]*1_100_010
isprime[0]=0
isprime[1]=0
if n==1:
    print(1)
    exit()
for i in range(2,1_100_010):
    if isprime[i]==1:
        j=2*i
        while 1_100_010>j:
            isprime[j]=0
            j+=i
prime=list()
for i in range(len(isprime)):
    if isprime[i]:
        prime.append(i)
m=n
b=m
while prime[-1]<m:
    Ll=list()
    for i in prime:
        if m%i==0:
            Ll.append(i)
    for i in Ll:
        m//=i
        m*=(i-1)
    if b==m:
        break
    else:
        b=m
L=list()
if prime[-1]<m:
    for i in prime:
        if n%i==0:
            L.append(i)
    for i in L:
        n//=i
        n*=(i-1)
    print(n*(b-1)//b)
else:
    for i in prime:
        if n%i==0:
            L.append(i)
    for i in L:
        n//=i
        n*=(i-1)
    print(n)

옛날에 짠 코드라서 약간(좀 많이) 스파게티다. 나중에 시간이 되면 더 깔끔한 코드로 업데이트 하겠다.