피보나치 수열 (Fibonacci Sequence)

피보나치 수열이란?

피보나치 수열 \((F_n)_{n \geq 0}\)은 다음과 같은 점화식으로 정의될 수 있다.

\[F_0=0, \space F_1=1, \quad F_n=F_{n-1}+F_{n-2} \space \space \forall n \geq 2\]

즉, 첫 두 항을 0과 1로 시작하고, 이후 각 항은 바로 이전 두 항의 합으로 정해지는 수열이 피보나치 수열이다.

역사적 배경

피보나치 수열의 이름은 13세기 이탈리아 수학자 레오나르도 피보나치(Leonardo Fibonacci)에서 유래된 것이다. 그는 1202년 <Liber Abaci>라는 책을 저술하면서 이 책에 토끼의 번식 문제를 통해 이 수열을 소개했다. 이 문제는 '토끼는 죽지 않고, 한 달 후 성숙하며, 성숙한 한 쌍의 토끼 사이에서는 한 달 후 새끼가 한 쌍 생긴다' 라는 이상적인 조건 하에서 한 쌍의 토끼가 한 달마다 새끼를 낳아 번식할 때 몇 달 후 토끼 쌍의 수가 얼마가 되는지는 묻는 것이었다. 피보나치는 이 문제를 소개하면서 자연스럽게 이 수열을 제시하게 된다.

피보나치 수열의 수학적 특성

이제 피보나치 수열에 대해 수학적으로 접근해나가보자. 피보나치 수열은 단순한 하나의 점화식을 통해 정의되지만, 이 수열은 정수론적 성질, 조합론적 해석, 합공식, 비대칭 성질 등에서 다양한 수학적 특성을 보이고 있다.

피보나치 수열의 부분합 관련 특성

피보나치 수열의 부분합 \(\sum\limits_{k=1}^n F_k\)는 다음과 같은 등식을 성립시킨다.

\[\sum_{k=0}^n F_k = F_{n+2} - 1\]

이제 위 식에 대해 수학적 귀납법을 이용하여 증명을 해보자.

\(n\)=0일 때, \(\sum\limits_{k=0}^0 F_k = F_0 = 0 = 1 - 1 = F_2 - 1 = F_{0+2} - 1\)이므로 성립한다.

\(n=N\)일 때, \(\sum\limits_{k=0}^N F_k = F_{N+2} - 1\)이 성립한다고 가정하자.

이제 \(n=N+1\)일 때 \(\sum\limits_{k=0}^{N+1} F_k = F_{N+3} - 1\)이 성립함을 보이면 증명이 완료된다.

\(\sum\limits_{k=0}^{N+1} F_k = (\sum\limits_{k=0}^N F_k) + F_{N+1} = (F_{N+2} - 1) + F_{N+1} = (F_{N+2} + F_{N+1}) - 1 = F_{N+3} - 1\)

따라서 위 식이 성립함을 증명하였다.

위 등식 외에도

\(\sum\limits_{k=0}^n F_{2k} = F_{2n+1} - 1\)

\(\sum\limits_{k=0}^n F_{2k+1} = F_{2n+2}\)

의 항등식들이 존재하고, 위와 같은 형식으로 증명이 가능하다.

파스칼 삼각형과의 관계

피보나치 수는 파스칼 삼각형 속에서도 드러난다. 특히 비스듬한 대각선의 합은 피보나치 수를 만들어낸다.

\[F_n = \sum_{k=0}^{\lfloor (n-1)/2 \rfloor} {{n-1-k} \choose k}\]

위 식은 조합과 큰 관련이 있는 파스칼 삼각형과 피보나치 수열 사이의 관계로, 피보나치 수가 조합론적으로도 해석 가능함을 보인다.

피보나치 수의 제곱의 합

\[\sum_{k=1}^n F_k^2 = F_n \cdot F_{n+1}\]

위 식은 피보나치 수의 제곱의 합이 곱 형태로 표현될 수 있음을 의미하며, 수학적 귀납법이나 점화식으로 증명할 수 있는데, 이제 수학적 귀납법을 이용하여 위 등식을 증명해보자.

\(n=1\)일 때, \(F_1^2 = 1 = F_1 \cdot F_2 = 1 \cdot 1 = 1\)

\(n=N\)일 때, \(\sum\limits_{k=1}^N F_k^2 = F_N \cdot F_{N+1}\)

이제 \(n=N+1\)일 때 위 등식이 성립함을 보이면 증명이 완료된다.

\(\sum\limits_{k=1}^{N+1} F_k^2 = (\sum\limits_{k=1}^{N} F_k^2) + F_{N+1}^2 = F_N \cdot F_{N+1} + F_{N+1}^2 = F_{N+1}(F_N + F_{N+1}) = F_{N+1} \cdot F_{N+2}\)

따라서, 위 등식이 성립함을 증명하였다.

짝수/홀수 및 배수성 성질

피보나치 수열은 위치에 따라 나머지 성질이 뚜렷이 나뉜다.

• \(F_n\)은 3의 배수일 조건 : \(n \equiv 0 \pmod 4 \)인 많은 경우 성립
• \(F_n\)은 2의 배수일 조건 : \(n \equiv 0 \pmod 3 \)
• 주기적으로 기우성(홀짝성)이 바뀌는 패턴이 존재하고, 이를 통해 빠르게 성질을 파악할 수 있음

유클리드 알고리즘과의 관련

피보나치 수열은 유클리드 알고리즘에서 가장 느리게 수렴하는 케이스를 만든다. 즉,

\[\gcd(F_n, F_{n+1}) = 1 \]

이며, 피보나치 수 \(F_n\), \(F_{n+1}\)을 입력으로 넣으며 유클리드 알고리즘은 정확히 \(n\)번의 단계가 걸린다. 이는 유클리드의 알고리즘의 최악 시간 복잡도와 직접적인 연결을 가지며, 계산 이론에 영향을 미치고 있다.

파르티션 해석 및 타일링 문제

피보나치 수는 조합론적인 타일링 문제에서도 등장한다. 예를 들어, \(1 \times n\) 직사각형을 \(1 \times 1\) 정사각형 또는 \(1 \times 2\) 도미노로 채우는 방법의 수는 정확히 \(F_{n+1}\)이고, 이는 점화식과 직접 연결된다.

길이 \(n\)에서,

• 마지막 조각이 \(1 \times 1\)인 경우 : \(n-1\) 길이의 타일링에 1 추가 \(\rightangle \F_n\)
• 마지막 조각이 \(1 \times21\)인 경우 : \(n-2\) 길이의 타일링에 2 추가 \(\rightangle \F_{n-1}\)

따라서 다음 점화식이 성립하게 되어 그 방법의 수가 정확히 \(F_{n+1}\)이 되는 것이다.

\[T_n = T_{n-1} + T_{n-2}, \quad T_0 = 1, T_1=1 \quad \rightarrow T_n = F_{n+1}\]

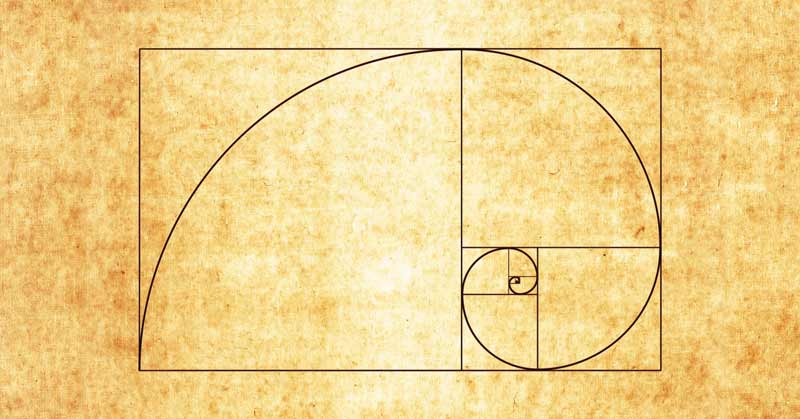
지수 성장 속도와 근사치

피보나치 수는 지수적으로 증가하며, \(F_n \approx \frac{1}{\sqrt{5}} {\phi}^{n} \)의 근사식이 적용된다. 이를 통해서 이 수열의 크기를 추정할 수 있게 된다. 정확히는

\[{\phi}^{n-2} < F_n < {\phi}^{n-1}, \quad n \geq 3\]

이는 수열의 지수 성장률을 보여주고, 정보 이론이나 계산 복잡도 이론에서 이용된다.

피보나치 수열의 일반항

이 파트에서는 피보나치 수열의 일반항을 구하는 대표적인 방법 두 가지를 소개하고자 한다.

생성함수를 이용한 방법

수열 \(\{F_n\}_{n=0}^{\infty}\)의 표준 생성함수 \(G(x)\)를 다음과 같이 정의한다.

\[G(x) = \sum_{n=0}^{\infty} F_n x^n\]

점화식을 이용하여 \(G(x)\)를 변형하고 다음과 같은 식을 고려한다.

\[G(x) = F_0 + F_1 x + F_2 x^2 + F_3 x^3 + \cdots\]

이제, \(xG(x), x^2G(x)\)를 구한다.

\[xG(x) = F_0 x + F_1 x^2 + F_2 x^3 + F_3 x^4 + \cdots\]

\[x^2G(x) = F_0 x^2 + F_1 x^3 + F_2 x^4 + \cdots\]

이를 통해 다음 식을 얻을 수 있다.

\[G(x) - x G(x) - x^2 G(x) = F_0 + (F_1 - F_0)x + (F_2 - F_1 - F_0)x^2 + \cdots\]

이 때, 피보나치 수열의 점화식 \(F_n = F_{n-1} + F_{n-2}\)에 의해, 위 식의 모든 계수는 0이 되며, \(F_0=0, F_1=1\)임을 대입하면, 다음이 유도된다.

\[G(x)(1 - x - x^2) = x \quad \Rightarrow \quad G(x) = \frac{x}{1 - x - x^2}\]

이제 위 생성함수에서의 분모 다항식을 인수분해한다.

방정식 \(1 - x - x^2 = 0\)의 해는
\[x = \phi = \frac{1 + \sqrt{5}}{2}, \quad \overline{\phi} = \frac{1 - \sqrt{5}}{2}\]
따라서,
\[G(x) = \frac{x}{(1 - \phi x)(1 - \overline{\phi} x)}\]

부분분수 분해를 통해
\[\frac{x}{(1 - \phi x)(1 - \overline{\phi} x)} = \frac{A}{1 - \phi x} + \frac{B}{1 - \overline{\phi} x}\]
양변에 공통 분모를 곱하면
\[x = A(1 - \overline{\phi} x) + B(1 - \phi x) = (A + B) - x (A \overline{\phi} + B \phi)\]
계수 비교를 통해
\[A + B = 0 \Rightarrow B = -A,\quad -A \overline{\phi} + A \phi = 1 \Rightarrow A(\phi - \overline{\phi}) = 1\]
\[\phi - \overline{\phi} = \frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2} = \sqrt{5} \Rightarrow A = \frac{1}{\sqrt{5}},\quad B = -\frac{1}{\sqrt{5}}\]

따라서 생성함수는 다음과 같이 전개된다
\[G(x) = \frac{1}{\sqrt{5}} \cdot \frac{1}{1 - \phi x} - \frac{1}{\sqrt{5}} \cdot \frac{1}{1 - \overline{\phi} x}\]

등비급수 전개로부터:
\[\frac{1}{1 - r x} = \sum_{n=0}^\infty r^n x^n \quad (|x| < 1/|r|)\]
\[G(x) = \sum_{n=0}^\infty \left( \frac{1}{\sqrt{5}} \phi^n - \frac{1}{\sqrt{5}} \overline{\phi}^n \right) x^n\]
따라서 일반항은 다음과 같다
\[F_n = \frac{1}{\sqrt{5}} \left( \phi^n - \overline{\phi}^n \right)\]

특성방정식을 이용한 방법

이 방법은 이차 선형 동차 점화식을 해석적으로 푸는 방식이라 할 수 있다.
피보나치 수열은 다음 점화식을 따른다:
\[F_n = F_{n-1} + F_{n-2}\]
이는 계수가 일정한 2차 선형 동차 점화식이며, 일반해는 다음과 같은 형태를 가진다
\[F_n = A r_1^n + B r_2^n\]
여기서 \( r_1, r_2 \)는 특성방정식의 두 근이다.
점화식에 대응하는 특성방정식은 다음과 같다
\[r^n = r^{n-1} + r^{n-2} \Rightarrow r^2 = r + 1 \Rightarrow r^2 - r - 1 = 0\]
이 방정식의 두 실근은 다음과 같다
\[r_{1,2} = \frac{1 \pm \sqrt{5}}{2} = \varphi, \ \bar{\varphi}\]
따라서 일반해는 다음과 같이 쓸 수 있다
\[F_n = A \varphi^n + B \bar{\varphi}^n\]
초기 조건은 다음과 같다
\[F_0 = 0 = A + B \]
\[F_1 = 1 = A \varphi + B \bar{\varphi}\]
첫 번째 식에서
\[A + B = 0 \Rightarrow B = -A\]
이를 두 번째 식에 대입하면
\[A \varphi - A \bar{\varphi} = A(\varphi - \bar{\varphi}) = 1\]
\[\Rightarrow A = \frac{1}{\varphi - \bar{\varphi}} = \frac{1}{\sqrt{5}}\]
따라서
\[A = \frac{1}{\sqrt{5}}, \quad B = -\frac{1}{\sqrt{5}}\]
따라서, 피보나치 수열의 일반항은 다음과 같다:
\[F_n = \frac{1}{\sqrt{5}} \left( \varphi^n - \bar{\varphi}^n \right)\]
여기서 \( \varphi = \frac{1 + \sqrt{5}}{2} , \bar{\varphi} = \frac{1 - \sqrt{5}}{2} \)이다.

요약

피보나치 수열의 일반항은

\[F_n = \frac{1}{\sqrt{5}} \left(\left(\frac{1+\sqrt{5}}{2} \right)^n - \left(\frac{1-\sqrt{5}}{2} \right)^n \right)\]

현대 수학에서의 피보나치 수열

모듈러 연산과 피사노 주기 (Pisano Period)

피보나치 수열을 어떤 정수 \(m\)에 대해 모듈러 연산을 적용하면, 수열은 반드시 유한한 주기를 가진다.

\[F_n  \mod  m\]

은 항상 어떤 \(T\)에 대해 \(F_{n+T} \equiv F_n \pmod m \)을 만족한다. 이 최소 주기 \(T\)를 피사노 주기라 한다.

예시:

• \(m = 2 \Rightarrow 주기 \space T = 3: 0, 1, 1, 0, 1, 1, \ldots \)
• \(m = 3 \Rightarrow 주기 \space T = 8: 0, 1, 1, 2, 0, 2, 2, 1, \ldots\)

성질:

• 피사노 주기는 항상 유한하다.
• 수론적 알고리즘 및 난수 생성기, 해싱 등에 응용됨
• 소수 \(p\)에 대해 \(\pi(p)\)의 성질은 아직 완전히 밝혀지지 않음

행렬 표현과 로그 시간 계산

피보나치 수열은 다음 행렬을 이용해 효율적으로 계산할 수 있다.

\[\begin{bmatrix} F_{n+1} \\ F_n \end{bmatrix} = \begin{bmatrix} 1 & 1 \\ 1 & 0 \end{bmatrix}^n \begin{bmatrix} 1 \\ 0 \end{bmatrix}\]

이 방법은 다음의 파트에서 유용하게 작용한다.

• 시간 복잡도 \(O(\log n)\): 지수 계산을 반복 제곱법(exponentiation by squaring)으로 수행 가능.
• 알고리즘적 효율성: 대형 피보나치 수 계산에 효과적.

고유값 분석:

행렬의 고유값은 \(\phi, \overline{\phi}\)이며, 이를 통해 행렬의 대각화가 가능하고, 일반항 도출로 이어질 수 있다.

수론적 성질

피보나치 수열은 수론적으로 흥미로운 여러 성질을 가진다. 대표적인 예는 다음과 같다

• 최대공약수: \(\gcd(F_m, F_n) = F_{\gcd(m,n)}\).이는 피보나치 수열이 유클리드 호제법과 밀접하게 관련됨을 보여준다
• 소수 판정 및 합동 조건:
  피보나치 수 중 특정 조건을 만족하는 수만이 소수가 될 수 있다. 예를 들어, \(F_p\)이 \(p\)가 소수일 때 \(p\)로 나누어떨어지는 경우는 매우 특별한 조건에서만 성립한다.
• 짝수 항과 홀수 항:
  모든 3번째 피보나치 수는 짝수이다. 즉, \(F_{3k} \equiv 0 \pmod{2}\).

일반화와 응용

• 루카 수열(Lucas sequence):
  루카 수열은 피보나치 점화식과 동일하지만 초기 조건이 다른 수열이다. \(L_0 = 2, L_1 = 1\)
• 피보나치 다항식:\(F_n(x) = x F_{n-1}(x) + F_{n-2}(x)\)으로 정의되며 조합론과 특이점 이론에서 응용될 수 있다.
• q-피보나치 수열:
  \(q\)-계수와 함께 정의되는 변형 수열로, 양자 수학과 특별 함수 이론에서 응용된다.