드디어 때가 왔다. 오늘은 \( y=e^x\)와 같은 초월함수를 근사하는 방법에 대하여 알아보자. 이를 위해서는 테일러 급수라는 매우 신기한 급수를 알아야 하는데, 오늘은 이것에 대해 알아보고, 증명하며, 활용해본다.

시작하자.

I. 초월함수란 무엇인가?

초월함수란 이름에서 알 수 있듯이 다항함수로 나타내지 못하는 함수들을 뜻한다. 대표적인 예시로는 아래의 것들이 있다.

\[ y=sin(x)\]

\[ y=cos(x)\]

\[ y=e^x\]

\[ y=ln(x)\]

이런 함수들은 얼핏 보면 도대체 어떻게 근사해야할지 감이 안잡힌다. 하지만 우리의 영혼의 단짝(?) 미분을 대려와서 생각해보자.

II. 테일러 급수의 아이디어의 이해

내가 잠시 어떤 점에 빙의해서, 함수상에 어떤 점에 서있다고 하자. 함수식을 알기는 하지만, 내가 무슨 이유에서 초월함수를 그리지 못해 어떻게 생겼는지는 모르겠다고 하자.

자, 이 상황에서 내가 이 함수를 그리려면 무엇이 필요할까? 나한테 어떤 마법의 상자가 있어서 그 안에 함수를 집어넣으면 함수의 각 지점에서의 기울기를 나타내는 함수를 돌려주는 상자가 있다고 하자.(눈치 빠른 독자라면 이것이 미분하는 행위에 해당한다는 것을 바로 알 수 있을 것이다.)

만약 내가 가진 함수가 \( y=sin(x)\)이고, 내가 서있는 지점이 \( x=0\)이라면, 상자에 집어넣은 다음 나온 함수에 내 위치을 집어넣으면 1이 나올 것이다. 원점에서 함수가 y=x와 비슷한 기울기로 증가하고 있다는 것을 뜻한다. 이를 다시 마법의 상자에 집어넣은다음 내 위치를 집어넣으면 0이 나온다. 여기서 기울기의 변화가 0이라는 것이다.

생각해보자. 내가 이 과정을 무한히 반복해서 기울기의 변화의 변화의 변화의 \( \cdot \cdot \cdot\) 변화를 구했다고 생각해보자. 이 정보를 가지면 내가 내 함수를 완벽하게 그릴 수 있을 것이다. 이것이 바로 테일러 급수의 기본 원리이다.

III. 테일러 급수 일반식의 유도

Step 1. Declaration

우리가가 최종적으로 원하는 함수가 \( y=f(x)\)라고 하자. 그리고 우리가 유도할 테일러 급수로 만들어낸 다항식을 \( y=g(x)\)라고 하자. 시행을 무한번 반복한다면 이론상

\[ f(x)=g(x)\]

이다. 위에서 말한 "나의 위치"를 여기서는 함수 정의역 상에 존재하는 어떤 점 \( x=a\)라고 하자. 우리는 이 \(a\)를 중심으로 \( f(x)\)를 근사할 것이다. 그리고 증명의 편의상 \( g(x) = a_0 + a_1 (x-a)+a_2 (x-a)^2 + a_3 (x-a)^3 \cdot \cdot \cdot\)이라고 하자.

Step 2. First Derivative

자, 이제 양변을 미분하자.

\[ f'(x) = g'(x) = a_1+2a_2 (x-a) + 3a_3 (x-a)^2 \cdot \cdot \cdot\]

여기서 \(x=a\)대입시 2번째 항 뒤의 모든 항이 전부 0이 된다는 사실은 자명하다. 이로부터 \(a_1 = f(a)\)를 알 수 있다. 나중에 되면 알겠지만, 규칙성을 위해 조금 더 잘 쓰자면,

\[a_1 = \frac{f(a)}{1!}\]

이다.

Step 3. Second Derivative

자 이제 위 식을 다시 미분하자.

\[ f''(x) = g''(x) = 2a_2 + 3a_3 (x-a)^2 \cdot \cdot \cdot\]

규칙이 보이는가? 여기서 \(x=a\)대입시 2번째 항 뒤의 모든 항이 전부 0이 된다는 사실은 (다시 한번) 자명하다. 이로부터 \(a_2\)를 표현하면,

\[a_2 = \frac{f(a)}{2!}\]

아까전에 규칙이 안보였다면 아마 이젠 보일거라 믿는다. 이제 일반화하자.

Step 4. Generalization

위 항들로부터 어느정도 식을 구했으니, 이제 일반화를 한번 해보자.

내가 \(a_n\)을 구하고 싶다면, 우산 Step 1의 식을 양변을 n번 미분한다.

\[ f^{(n)} (x) = g^{(n)} (x) = n!a_n + (n+1)! a_{n+1} (x-a) \cdot \cdot \cdot\]

여기서 \(x=a\)대입시 2번째 항 뒤의 모든 항이 전부 0이 된다. 따라서 이로부터 다음과 같은 사실을 알 수 있다.

\[a_n = \frac{f(a)}{n!}\]

즉, 원래 함수인 \(f(x)\)는 이렇게 쓸 수 있다 :

\[ f(x) = \sum_{n=0}^{\infty} C_n x^n \]

\[\text{where }C_n = \frac{f^{(n)} (a)}{n!}\]

IV. 좀 신기한 것들

A. 테일러 급수의 정확도

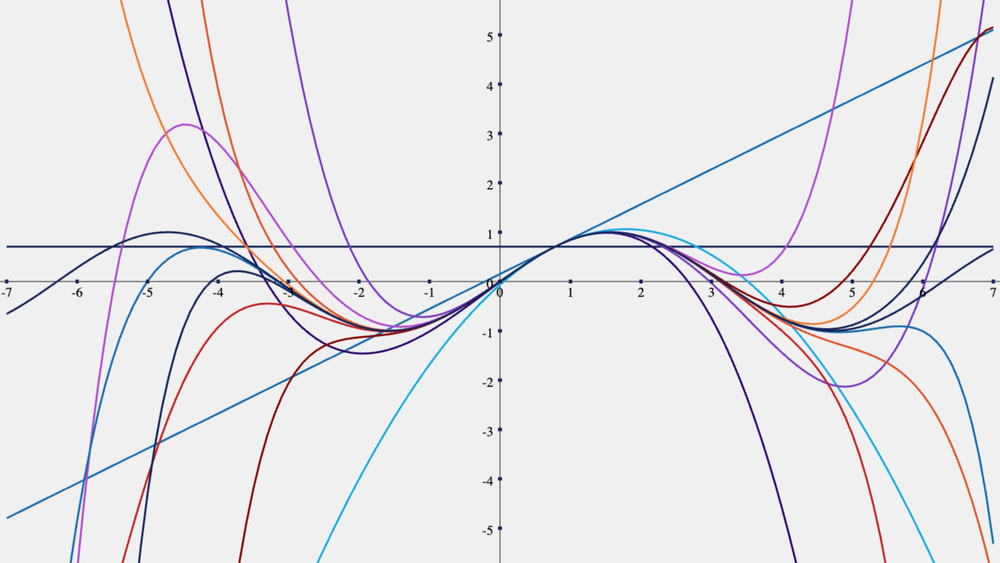
당연한 이야기겠지만, 우리는 무한대 항까지 테일러 급수를 계산할 수 없다. 따라서 적당한 지점에서 테일러 급수를 끊게 되는데, 이 경우 필연적으로 약간의 오차가 생긴다. 아래의 두개의 그래프는 각각 \(y=e^x\)와 \(y=sin(x)\)의 테일러 전개 항 수에 따른 근사 지점으로부터 0.1만큼 떨어진 지점에서 측정한 오차이다.

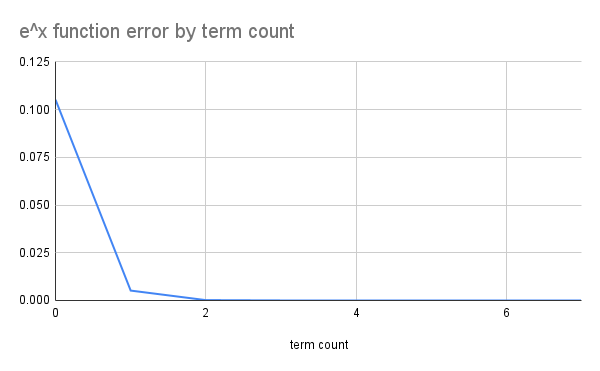
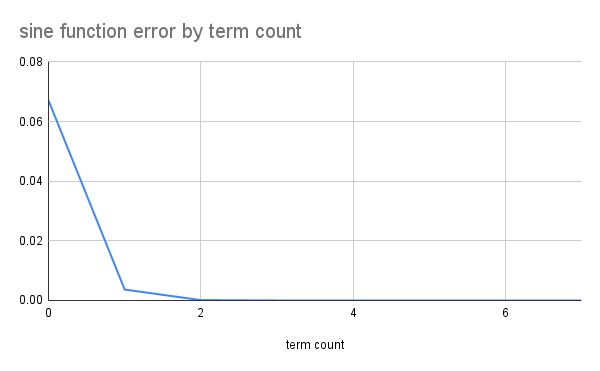
매우 신기하게도 오차가 기하급수적으로 감소하는 것을 알 수 있다.

원하는 독자가 있을까봐 위 함수들의 테일러 급수 항 수에 따른 함수 모양 또한 아래 있다.

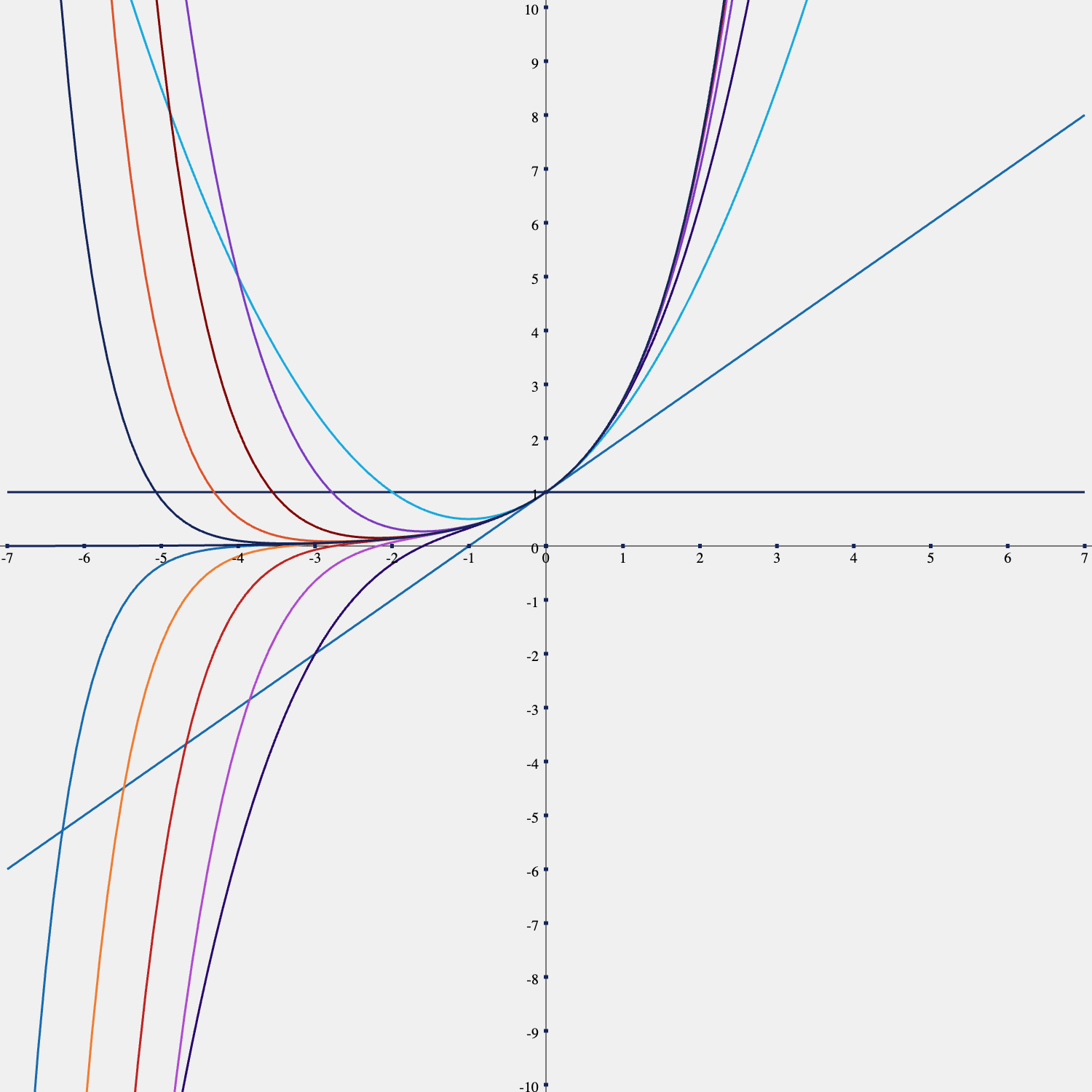
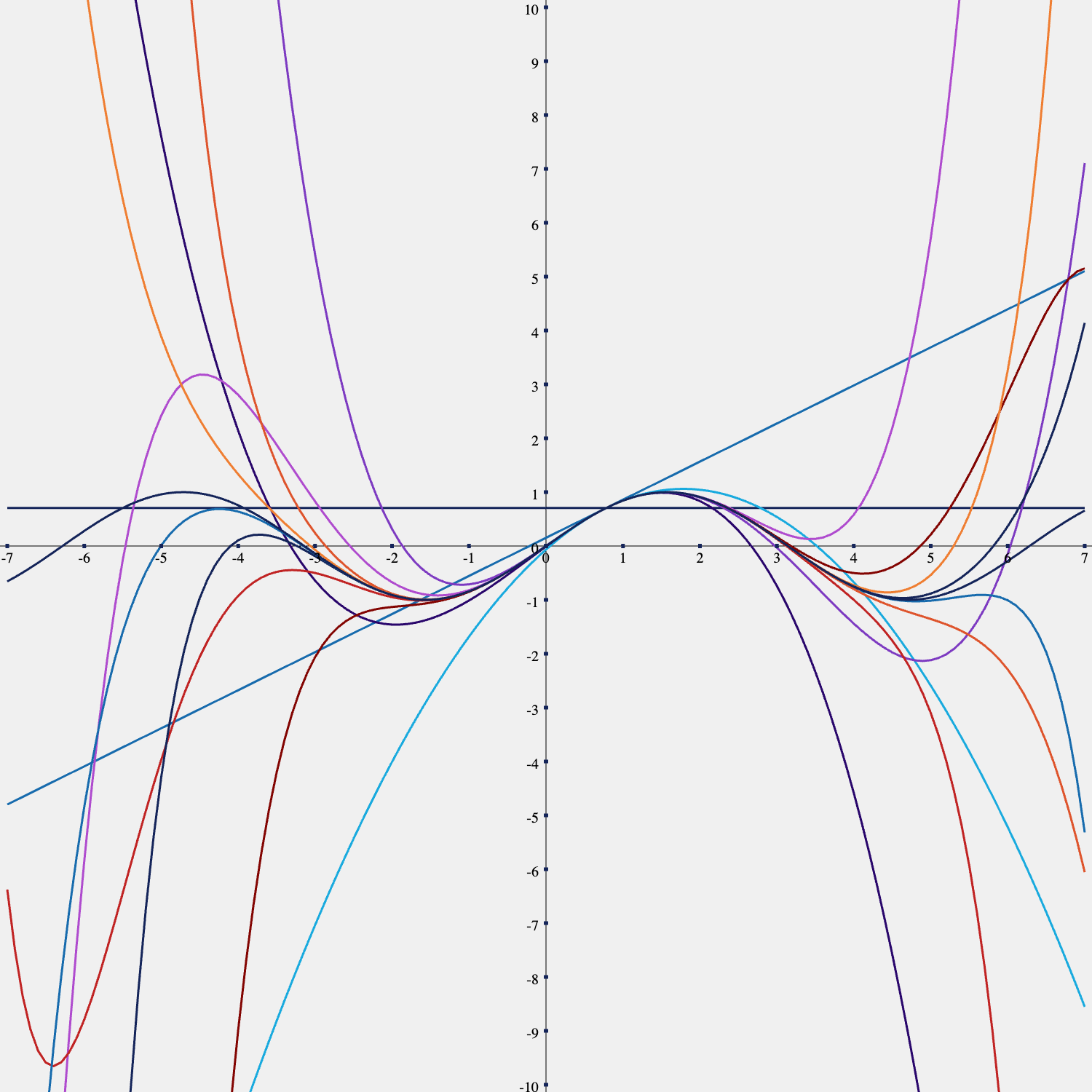
B. 매클로린 급수

매클로린 급수는 테일러 급수중 기준점 \(a=0\)인 급수들을 의미한다. \((x-a)\)항을 같이 가지고 다닐 필요가 없기 때문에 증명이 가장 깔끔해 보인다.

C. 활용

테일러 급수는 생각보다 많은 곳에서 활용이 된다. 몇가지 예시를 알아보자.

i) Simulation

내 최근 글을 읽어본 사람이라면 내가 Runge Kutta 알고리즘에 대하여 작성한 글 또한 읽어보았을 것이다. (안 읽어보았고 심심하거나 궁금하면 읽어보는 것을 추천한다.) 여기 증명에서 테일러 급수가 사용되는데, 이것이 공식적인 증명방법일 만큼 강력한 급수이다. (이는 사실 2번에도 약간 해당되긴 한다.)

ii) Mathematical Proof

테일러 급수는 수학적 증명에서도 셀 수 없이 많이 사용된다. 내가 옛날에 올린 글 중 오일러의 공식을 증명하는 과정에서 테일러 급수를 이용하는 것을 보인 적이 있다. (이 또한 궁금하면 읽어보는 것을 추천한다.) 또한 삼각함수를 좀 가지고 놀아본 사람이라면 한번쯤은 들어봤을 공식인

\[\lim_{x\to0}\frac{\sin(x)}{x}=1\]

또한 엄청 쉽게 증명할 수 있다. 글이 너무 길어지고 있는 관계로 증명은 아래 내가 옛날에 썼었던 보고서를 별첨해놓았으니 참고바란다.

V. 결론

내가 수학을 오래 공부한 것은 아니지만, 장담하건데 테일러 급수는 FFT와 함께 (내가 아는 한에서는) 실용수학에서 가장 많이 사용되는 공식이 아니지 않을까 싶다.

이 글의 내용과 나오는 증명들은 내가 옛날에 학교에서 진행했던 탐구의 내용을 일부 참고하였다. 이에 대해서 더 알고 싶은 독자들은 이 링크를 참고하길 바란다.