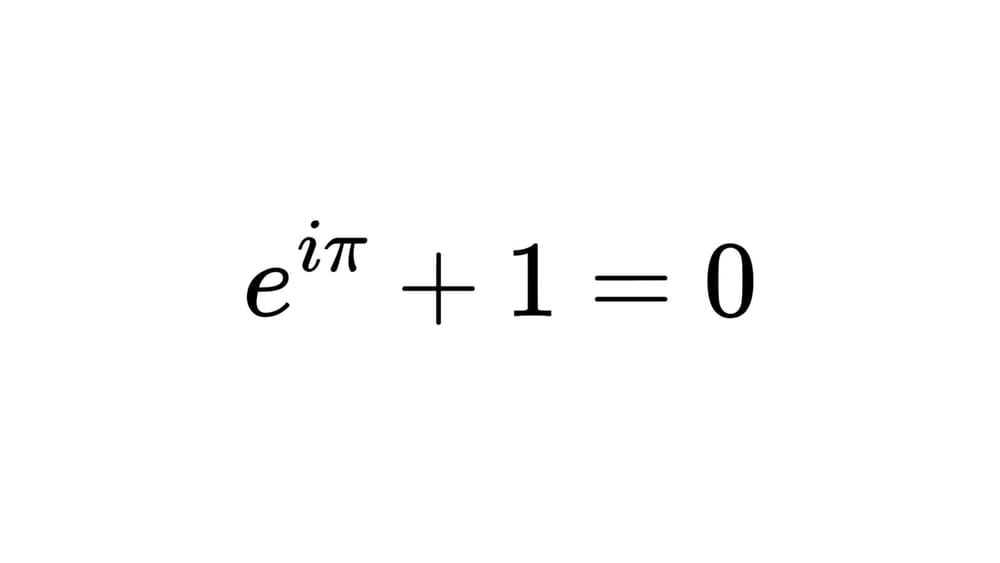#euler #formula #taylor-series #quotients

아주 유명한 공식 중에 다음과 같은 것이 있다.

\[ e^{i\pi} + 1 = 0\]

대충 봐서는 이상하다. 저게 어떻게 성립하는 걸까?

저 식을 이해하기 위해서는, 오늘의 최종 목적이기도 한, 아래의 식(오일러의 공식)을 이해해야 한다.

\[ e^{i\theta} = cos(\theta)+isin(\theta)\]

시작하자.

Part I. Proof by Power Series

수학에 관심이 좀 있다면 테일러 급수라는 것에 대하여 들어본 적이 있을 것이다. 간단히 설명하자면, 어떤 점을 기준으로 하여 원래는 다항함수로 못 나타내는 함수(삼각함수, 지수함수 등)을 다항함수로 "근사"하게 해주는 방법이다. 그 원리는 어떤 점에서의 값, 도함수의 값, 이계도함수의 값, 등등등...을 같게 만드는 방식이다.

테일러 급수의 일반식은 다음과 같은 형태이다 :

\[\text{For a random function }f(x)\text{, we can define }f(x) = \sum_{n=0}^{\infty}\frac{f^{(n)}(a)}{n!}(x-a)^n \]

만약 테일러 급수에 대하여 더 자세히 알아보고 싶다면 이 영상을 참고하자. 이때 위 식에서 \(a = 0 \) 을 대입한 것을 매클로린 급수라고 한다.

자, 이제 \( f(\theta) = e^{i\theta}\) 를 \(\theta=0 \) 에서 근사해보자.

\[ f(\theta) = e^{i\theta} \approx1 + i\theta + \frac{(i\theta)^2}{2!} + \frac{(i\theta)^3}{3!} + \frac{(i\theta)^4}{4!} + \frac{(i\theta)^5}{5!} + \cdot \cdot \cdot \]

여기서 \(i \)를 정리해주면

\[ f(\theta) = e^{i\theta} \approx1 + i\theta - \frac{\theta^2}{2!} - \frac{i\theta^3}{3!} + \frac{\theta^4}{4!} + \cdot \cdot \cdot \]

가 된다.

자, 이제 비슷한 방법으로 \( cos(x), sin(x)\) 도 근사하자. \( cos(x), sin(x)\) 는 \(n\)계도함수가 반복되므로 이 점을 활용하자.

\[ sin(\theta) \approx \theta - \frac{\theta^3}{3!} + \frac{\theta^5}{5!} + \cdot \cdot \cdot \]

\[ cos(\theta) \approx 1 - \frac{\theta^2}{2!} + \frac{\theta^4}{4!} + \cdot \cdot \cdot \]

우리가 위에서 전개한 식들을 잘 살펴보자. 여기서부터 우리는

\[ e^{i\theta} = cos(\theta)+isin(\theta ) \]

임을 알 수 있다.

Part II. Proof by Quotients

이번 증명은 좀 방식이 특이하다. 이미 위 식을 알고 있다는 전제하에 이것이 항상 성립함을 밝힐 것이다.

우선, 다음과 같은 함수 \( g(\theta)\)를 정의하자.

\[ g(\theta) = \frac{cos(\theta)+isin(\theta )}{ e^{i\theta}}\]

\[ = (cos(\theta)+isin(\theta ))e^{-i\theta}\]

이것을 미분하자. 곱의 미분을 사용해주면 된다.

\[ g'(\theta) = (-sin(\theta)+icos(\theta ))e^{-i\theta} - (cos(\theta)+isin(\theta ))ie^{-i\theta}\]

\[= 0\]

이것으로 \( g(\theta)\)는 상수함수임을 알 수 있다. 이때 \( \theta = 0\)을 대입시

\[ g(0) = 1\]

임을 알 수 있다. 따라서 \(g(\theta) \)의 모든 값이 1이므로 \(e^{i\theta} \)와 \(cos(\theta)+isin(\theta )\) 가 항상 같다는 것을 알 수 있다.

Part III. Euler's Identity

서론에 나왔던 식으로 돌아가자.

\[ e^{i\pi} + 1 = 0\]

이것은 어떻게 성립하는 것일까? 두가지 방법으로 알아보자.

Part III - I) Complex Plane Approach

우리가 구한 오일러의 공식(\( e^{i\theta} = cos(\theta)+isin(\theta ) \))은 복소평면 상에서는 무엇을 의미할까? 조금만 생각해본다면 이것이 원의 방정식임을 알 수 있다. 여기에 \(\pi\)를 대입한다는 것은 동경을 기준으로 하여 180도 회전 시킨 점이므로 실수축의 -1에 해당한다. (어렵다면 아래 그림을 참조하자.)

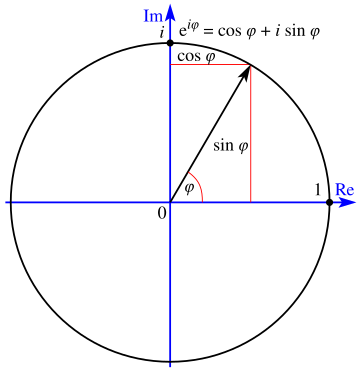
Part III - II) Value Approach

두번째 방법은 간단하다. \(\theta\)에 그냥 바로 \(\pi\)를 대입해보자. -1이 나오는 것을 알 수 있다.

이것으로 오늘은 오일러의 유명한 공식에 대하여 간단하게나마 알아보았다.